
An earlier tutorial showed how the distance between two notes (called an interval) can be named depending on its size (i.e. the number of semitones between the notes). For example, an interval of 7 semitones can be called a "perfect fifth", such as the interval between C and G:
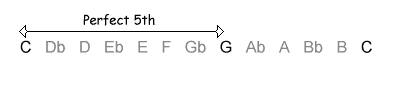
However, it is not totally correct to say that the interval between C and G will always be 7 semitones, a perfect fifth. This is only true where C is the lower of the two notes. The interval may be inverted by moving C up by an octave (or, conversely, moving G down by an octave):
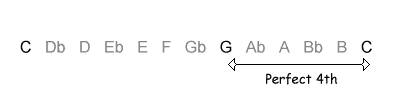
This interval is a perfect fourth, 5 semitones.
Bear in mind here that we are talking only about moving pairs of notes around within the octave, not extending an interval beyond an octave by moving the higher note up by 12 semiones, or the lower note down by 12 semitones. Such extended intervals will be the subject of a future tutorial.
The following table shows the intervals within an octave, with their inversions. Note that when the size of the first interval increases, the size of the inverted interval decreases. NB, the interval of a diminished fifth contains the same number of semitones as its inversion, an augmented fourth.
| 0 / 12 semitones | 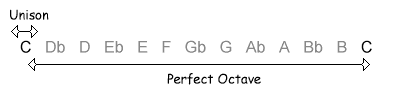 |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 / 11 semitones | 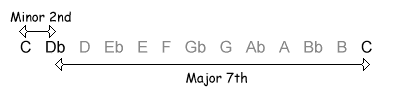 |
||||||||
| 2 / 10 semitones | 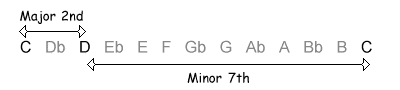 |
||||||||
| 3 / 9 semitones | 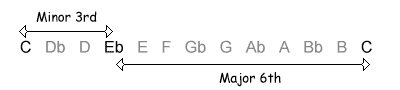 |
||||||||
| 4 / 8 semitones | 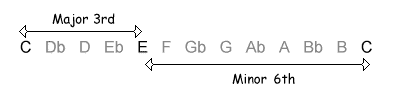 |
||||||||
| 5 / 7 semitones | 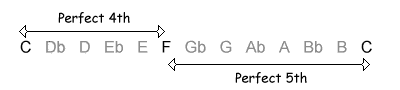 |
||||||||
| 6 / 6 semitones | 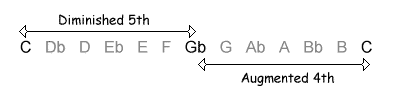 |
||||||||
| 7 / 5 semitones | 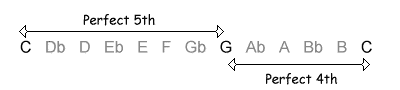 |
||||||||
| 8 / 4 semitones | 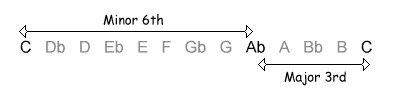 |
||||||||
| 9 / 3 semitones | 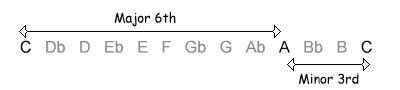 |
||||||||
| 10 / 2 semitones | 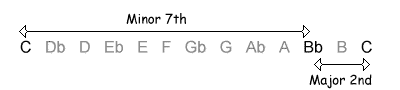 |
||||||||
| 11 / 1 semitones | 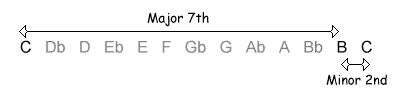 |
| Product/Info... | PhatPhish Application | | | Product Help | | | GUPPY - PhatPhish for the web | | | About The Author |
|---|
| Get Stuff... | Download PhatPhish | | | Mechandise | | | Blank Stave And Tab Sheets | | | Tutorials |
|---|
| Do Stuff... | Register | | | Feedback | | | Links | | | Donate | | | Ask A Question |
|---|
| Social Media... | YouTube | | | | |
|---|
| Promote... | Spread The Word | | | Posters/Flyers |
|---|
| Play... | PhatPhish Picks - Boutique Plectrums |
|---|
| ©2002-2022, Dave Dixon / CyberFlotsam http://www.cyberflotsam.com |